2021 AMC 10A 试题/第1题
题目
求值
\[ \left( {{2}^{2} - 2}\right) - \left( {{3}^{2} - 3}\right) + \left( {{4}^{2} - 4}\right) \]
\( \textbf{(A)}\;1\;\textbf{(B)}\;2\;\textbf{(C)}\;5\;\textbf{(D)}\;8\;\textbf{(E)}\;{12} \)
解法1
\[ \left( {4 - 2}\right) - \left( {9 - 3}\right) + \left( {{16} - 4}\right) = 2 - 6 + {12} = 8\text{. This corresponds to (D) 8} \]
-happykeeper
解法2
\[ \left( {{2}^{2} - 2}\right) - \left( {{3}^{2} - 3}\right) + \left( {{4}^{2} - 4}\right) = 2\left( {2 - 1}\right) - 3\left( {3 - 1}\right) + 4\left( {4 - 1}\right) \]
\[ = 2\left( 1\right) - 3\left( 2\right) + 4\left( 3\right) \]
\[ = 2 - 6 + {12} \]
\[ = \text{(D) 8 .} \]
~MRENTHUSIASM
视频解法 #0(极快计算)
https://www.youtube.com/watch?v=m0_UMI2mnZs&list=PLexHyfQ8DMuKqltG3cHT7Di4jhVl6L4YJ&index=2~北美数学竞赛冲冲冲
2021 AMC 10A 试题/第2题
题目
Portia(波西亚)的高中学生人数是Lara(劳拉)高中的3倍。两所高中共有2600名学生。Portia的高中有多少名学生?
(A) 600 (B) 650 (C) 1950 (D) 2000 (E) 2050
解法1
可建立如下方程组,其中 \( p \) 表示Portia高中的学生人数, \( l \) 表示Lara高中的学生人数。
\[ p = {3l} \]
\[ p + l = {2600} \]
将 \( p \) 用 \( {3l} \) 替换后得到 \( {4l} = {2600} \) 。解 \( l \) 得 \( l = {650} \) 。由于需求 \( p \) ,我们将650乘以3得到 \( p = {1950} \) ,即 \( \left| C\right| \)
-快乐守护者
解法2(单变量)
假设Lara的高中共有 \( x \) 名学生,那么Portia的高中就有 \( {3x} \) 名学生。已知 \( x + {3x} = {2600}, \) 或 \( {4x} = {2600}. \) ,因此答案为
\[ {3x} = {2600}\left( \frac{3}{4}\right) = {650}\left( 3\right) = {650}. \]
~MRENTHUSIASM
解法3(算术法)
显然,2600名学生是Lara高中人数的4倍,因此Lara的高中有 \( {2600} \div 4 = {650} \) 名学生,而Portia的高中有 \( {650} \cdot 3 = 0 \) 名学生。
~MRENTHUSIASM
解法4(选项法)
解法4.1(快速检验)
Portia高中的学生人数必须是3的倍数,这排除了 \( \left( \mathbf{B}\right) ,\left( \mathbf{D}\right) , \) 和(E)。由于(A)太小(显然 \( {600} + {600}/3 < {2600} \) ),因此剩下(C) 1950
~MRENTHUSIASM
解法4.2(代入选项验证)
对于(A),我们有 \( {600} + \frac{600}{3} = {800} \neq {2600} \) ,因此(A)不正确。
对于(B),我们有 \( {650} + \frac{650}{3} = {866}\frac{2}{3} \neq {2600} \) ,因此(B)不正确。
对于(C),我们有 \( {1950} + \frac{1950}{3} = {2600} \) ,因此(C) 1950正确。为完整起见,我们还将检查选项(D)
和(E)。
对于(D),我们有 \( {2000} + \frac{2000}{3} = {2666}\frac{2}{3} \neq {2600} \) 。因此,(D)不正确。
对于(E),我们有 \( {2050} + \frac{2050}{3} = {2733}\frac{1}{3} \neq {2600} \) 。因此,(E)不正确。
2021 AMC 12A 试题/第3题
以下题目同时出现在2021年AMC 10A第3题和2021年AMC 12A第3题,因此两道题均重定向至此页面。
问题
两个自然数之和为17,402。其中一个数能被10整除。若将该数的个位数字擦除,便得到另一个数。求这两个数的差。
(A) 10,272 (B) 11,700 (C) 13,362 (D) 14,238 (E) 15,426
解决方案 1
10的倍数的个位数字总是0。每乘以10时,我们就在末尾添一个0。因此,去掉个位数字就等于除以10。
设较小的数(即去掉个位后得到的数)为 \( a \) ,则较大的数就是 \( {10a} \) 。
我们知道总和是 \( {10a} + a = {11a} \) ,因此 \( {11a} = {17402} \) 。于是 \( a = {1582} \) 。差值为 \( {10a} - a = {9a} \) 。所以,答案是 \( 9\left( {1582}\right) = {14238} = \) (D)
-abhinavg0627
解法2(惰性速度)
因为10的倍数个位是0,所以另一个整数必须以2结尾,因为两个整数相加得到的数末位是2。因此,差的个位必须是 \( {10} - 2 = 8 \) ,而唯一末位是8的选项是(D) 14238
~酷木星 2021
另一个快速解法是将总和视为一个数 \( n \) 加上 \( {10n} \) 。差值为 \( {9n} \) ,即 \( \frac{9}{11} \) 的
给定的和。
解法3(竖式加法与逻辑推理)
设较大的数为 \( \overline{{AB},{CD0}} \) ,则较小的数为 \( \overline{A,{BCD}} \) 。竖式相加,我们有
| \( A \) | \( B \) | \( C \) | \( D \) | 0 | |
| + | \( A \) | \( B \) | \( C \) | \( D \) | |
| 1 | 7 | 4 | 0 | 2 |
从右往左计算,我们得到
\[ D = 2 \Rightarrow C = 8 \Rightarrow B = 5 \Rightarrow A = 1\text{.} \]
较大的数是15,820,较小的数是1,582,它们的差是
\( {15},{820} - 1,{582} = \left( {\mathbf{D}\mathbf{)}{14},{238}}\right) \) .
2021 AMC 10A 试题/第4题
题目
一辆小车沿山坡下滑,第一秒行驶5英寸,并以每过1秒就比前一秒多行驶7英寸的加速度加速。小车共用时30秒到达坡底。问:小车行驶的总距离是多少英寸?
(A) 215 (B) 360 (C) 2992 (D) 3195 (E) 3242
解法1(等差数列)
因为
距离 \( = \) 速度 \( \times \) 时间,
我们需求的是和
\[ 5\left( 1\right) + {12}\left( 1\right) + {19}\left( 1\right) + {26}\left( 1\right) + \cdots = 5 + {12} + {19} + {26} + \cdots , \]
其中共有30个加数。最后一个加数是 \( 5 + 7\left( {{30} - 1}\right) = {208}. \) 因此,所求的和为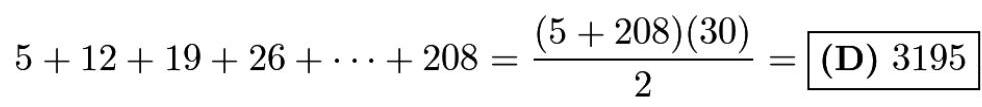
回忆等差数列求和公式:取首项与末项的平均值,再乘以项数,即
\[ \frac{\text{First} + \text{Last}}{2} \cdot \text{Count.} \]
~MRENTHUSIASM
解法2(选项与模运算)
由前一种解法中的30项和
\[ 5 + {12} + {19} + {26} + \cdots \]
取模10得
\[ 5 + {12} + {19} + {26} + \cdots \equiv 3\left( {0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9}\right) = 3\left( {45}\right) \equiv 5\;\left( {\;\operatorname{mod}\;{10}}\right) . \]
唯一满足 \( 5{\;\operatorname{mod}\;{10}} \) 的选项是(A)和(D)。粗略估算可知,(A)太小,因此答案为(D) 3195
2021年AMC 10A试题/第5题
问题
一个共有 \( k > {12} \) 名学生的班级的测验平均分为8。其中12份测验的平均分为14。问:剩余测验的平均分用 \( k \) 表示是多少?
(A) \( \frac{{14} - 8}{k - {12}} \) (B) \( \frac{{8k} - {168}}{k - {12}} \) (C) \( \frac{14}{12} - \frac{8}{k} \) (D) \( \frac{{14}\left( {k - {12}}\right) }{{k}^{2}} \) (E) \( \frac{{14}\left( {k - {12}}\right) }{8k} \)
解法1(广义)
班级总分为 \( {8k}. \) ,12次小测总分为 \( \underline{{12} \cdot {14} = {168}.} \) ,因此剩余 \( k - {12} \) 次小测的总分为 \( {8k} - {168} \) ,其平均分为 \( \left( \mathbf{B}\right) \frac{{8k} - {168}}{k - {12}} \) 。~MRENTHUSIASM
解法2(便利取值与观察)
集合 \( k = {13} \) 。答案与上一位学生的测验分数相同,即 \( 8 \cdot {13} - {14} \cdot {12} < 0. \) 根据答案
在这些选择中,只有 \( \left( {\left( \mathrm{B}\right) \frac{{8k} - {168}}{k - {12}}}\right) \) 会使 \( k = {13} \) 产生负值。
~热情
解决方案 3
已知前12名学生的平均分为14,因此他们的总分是12×14=168。设其余学生的平均分(即待求值)为a。在总人数为 \( k \) 的班级中,剩余学生人数可表示为(k-12)。这些学生的总分为a(k-12),全班总分为168+a(k-12)(前12名学生加上其余学生)。全班平均分可表示为 \( \smallsetminus \) frac{168+a(k-12)}{k}。已知全班平均分为8,因此建立方程frac{168+a(k-12)}{k}=8,解出a(即(k-12)名学生的平均分)即可得到用k表示的答案:frac{8k-168}{k-12}。
2021年AMC 10A试题/第6题
问题
尚塔尔和让从一条小路的起点出发,前往一座消防塔。让背着沉重的背包,走得较慢。尚塔尔以每小时4英里的速度开始行走。走到塔的一半路程时,小路变得非常陡峭,尚塔尔减速至每小时2英里。到达塔后,她立即转身,以每小时3英里的速度沿陡峭路段下山。她在中点与让相遇。让在他们相遇前的平均速度是多少,单位为英里每小时?
(A) \( \frac{12}{13} \) (B) 1 (C) \( \frac{13}{12} \) (D) \( \frac{24}{13} \) (E) 2
解法1(广义距离)
设 \( {2d} \) 英里为起点到火塔的距离。当尚塔尔遇到让时,她已经行驶了
\[ \frac{d}{4} + \frac{d}{2} + \frac{d}{3} = d\left( {\frac{1}{4} + \frac{1}{2} + \frac{1}{3}}\right) = d\left( {\frac{3}{12} + \frac{6}{12} + \frac{4}{12}}\right) = \frac{13}{12}d \]
小时。让也行驶了 \( \frac{13}{12}d \) 小时,并且他行驶了 \( d \) 英里。因此,他的平均速度为
\[ \frac{d}{\left( \frac{13}{12}d\right) } = \left( {\mathbf{A})\frac{12}{13}}\right) \]
英里每小时。
~MRENTHUSIASM
解法2(具体距离)
我们使用与解法1相同的模板,只是将 \( \mathbf{d} \) 替换为一个具体数字。
设24英里为起点到火塔的距离。当尚塔尔遇到让时,她行驶了
\[ \frac{12}{4} + \frac{12}{2} + \frac{12}{3} = 3 + 6 + 4 = {13} \]
小时。让也行驶了13小时,并且他行驶了12英里。因此,他的平均速度为 \( 便{\_ \_ \_ } \) (A)13英里每小时
2021 AMC 12A 第4题
以下问题同时出现在2021 AMC 10A第7题和2021 AMC 12A第4题,因此两题均重定向至此页面。
问题
汤姆收集了13条蛇,其中4条是紫色的,5条是快乐的。他观察到:所有快乐的蛇都会加法;所有紫色的蛇都不会减法;所有不会减法的蛇也不会加法。关于汤姆的蛇,可以得出以下哪个结论?
(A) 紫色的蛇会加法。
(B) 紫色的蛇是快乐的。
(C)会加法的蛇是紫色的。
(D)快乐的蛇不是紫色的。
(E)快乐的蛇不会减法。
解法1
我们知道紫色蛇不会减法,因此也不会加法。由于快乐蛇必须会加法,紫色蛇就不可能是快乐的。因此,我们得知快乐蛇不是紫色的,答案是 \( \left| {\left( \mathrm{D}\right) \mid }\right| \)
-abhinavg0627
解法2(用箭头解释解法1)
已知
(1)快乐 \( \Rightarrow \) 会加法
(2)紫色 \( \Rightarrow \) 不会减法
(3)不会减法 \( \Rightarrow \) 不会加法
将(2)和(3)合并为下面的 \( \left( *\right) \) ,我们得到
(1)快乐 \( \Rightarrow \) 会加法
(*)紫色 \( \Rightarrow \) 不会减法 \( \Rightarrow \) 不会加法
显然,答案是
2021 AMC 12A 试题/第5题
以下题目同时出现在2021年AMC 10A第8题和2021年AMC 12A第5题,因此两题均重定向至此页面。
题目
当一位学生将数字66乘以一个循环小数
\[ \underline{1} \cdot \underline{abab}\ldots = \underline{1} \cdot \overline{ab}, \]
其中 \( a \) 和 \( b \) 为数字,他没有注意到循环记号,而是直接计算了66×[1.a, b]。后来他发现所得结果比正确答案少了0.5。这个两位数 \( \underline{ab} \) 是多少?
(A) 15 (B) 30 (C) 45 (D) 60 (E) 75
解答
已知 \( 0.\overline{ab} = \frac{ab}{99} \) 和 \( 0.{ab} = \frac{ab}{100} \) 。设 \( \overline{ab} = x \) 。我们有 \( {66}\left( {1 + \frac{x}{100}}\right) + {0.5} = {66}\left( {1 + \frac{x}{99}}\right) \) 。解得 \( {100x} - {75} = {99x} \) ,因此 \( x = 0 \) ,(E) 75。~aop2014
2021 AMC 12A 题目/第7题
以下题目同时出现在2021年AMC 10A第9题和2021年AMC 12A第7题,因此两题均重定向至此页面。
题目
对于实数 \( x \) 和 \( y \) , \( {\left( xy - 1\right) }^{2} + {\left( x + y\right) }^{2} \) 的最小可能值是多少?
(A) 0 (B) \( \frac{1}{4} \) (C) \( \frac{1}{2} \) (D) 1 (E) 2
解法1
展开后,表达式为 \( {x}^{2} + {2xy} + {y}^{2} + {x}^{2}{y}^{2} - {2xy} + 1 \) 或 \( {x}^{2} + {y}^{2} + {x}^{2}{y}^{2} + 1 \) 。根据平凡不等式(所有平方均非负),其最小值为 \( \left| {\mathrm{\left( D\right) }1}\right| \) ,可在 \( x = y = 0 \) 时取得。~aop2014
解法2(过度杀伤)
与解法1类似,将原式展开化简为 \( {x}^{2} + {y}^{2} + {x}^{2}{y}^{2} + 1 \) ,并设 \( f\left( {x, y}\right) = {x}^{2} + {y}^{2} + {x}^{2}{y}^{2} + 1 \) 。为求局部极值,需找出使 \( \nabla f\left( {x, y}\right) = \mathbf{0} \) 的点。首先,分别对 \( x \) 和 \( y \) 求一阶偏导,并令其为0:
\[ \frac{\partial f}{\partial x} = {2x} + {2x}{y}^{2} = {2x}\left( {1 + {y}^{2}}\right) = 0 \Rightarrow x = 0 \]
\[ \frac{\partial f}{\partial y} = {2y} + {2y}{x}^{2} = {2y}\left( {1 + {x}^{2}}\right) = 0 \Rightarrow y = 0 \]
因此,在(0,0)处存在一个局部极值。由于这是唯一的极值,我们可以假设这是一个最小值,因为题目要求的是最小值(尽管这也可以通过二阶偏导数检验法[partial second derivative test]加以证明),并且由于它是唯一的最小值,因此也是全局最小值,这意味着 \( f\left( {0,0}\right) \) 是 \( f\left( {x, y}\right) \) 的最小值。将(0,0)代入 \( f\left( {x, y}\right) \) ,我们得到1
\( \Rightarrow \) (D) 1
2021 AMC 12A 试题/第9题
以下问题同时出现在2021年AMC 10A第10题和2021年AMC 12A第9题,因此两道题均重定向至此页面。
问题
以下哪一项等价于
\[ \left( {2 + 3}\right) \left( {{2}^{2} + {3}^{2}}\right) \left( {{2}^{4} + {3}^{4}}\right) \left( {{2}^{8} + {3}^{8}}\right) \left( {{2}^{16} + {3}^{16}}\right) \left( {{2}^{32} + {3}^{32}}\right) \left( {{2}^{64} + {3}^{64}}\right) ? \]
(A) \( {3}^{127} + {2}^{127} \) (B) \( {3}^{127} + {2}^{127} + 2 \cdot {3}^{63} + 3 \cdot {2}^{63} \) (C) \( {3}^{128} - {2}^{128} \) (D) \( {3}^{128} + {2}^{128} \) (E) \( {5}^{127} \)
解决方案 1
你只需将整个方程乘以(3 - 2)。随后所有项都会通过平方差公式轻松化简,最终得到 \( {3}^{128} - {2}^{128} \) 或 \( C \) 。注意,你无需担心 \( 3 - 2 \) ,因为它等于1。——Lemonie
解决方案 2
如果你没能想到(3 - 2)这一洞察,也可以直接注意到答案能被 \( \left( {2 + 3}\right) = 5 \) 和 \( \left( {{2}^{2} + {3}^{2}}\right) = {13} \) 整除。接着,我们可以对选项使用费马小定理(Fermat’s Little Theorem) \( p = 5,{13} \) ,从而判断哪些选项同时被5和13整除。这就是 \( C \) 。
-喵托
解决方案3
展开前几项后,每一项之后的结果似乎为
\( {2}^{{2}^{n} - 1} + {2}^{{2}^{n} - 2} \cdot {3}^{1} + {2}^{{2}^{n} - 3} \cdot {3}^{2} + \ldots + {2}^{1} \cdot {3}^{{2}^{n} - 2} + {3}^{{2}^{n} - 1} \) 其中n为展开的项数。我们可以用数学归纳法证明这一点。基础步骤显然成立。当再展开一项时,所有前项乘以 \( {2}^{{2}^{n - 1}} \) 将得到 \( {2}^{{2}^{n} - 1} + {2}^{{2}^{n} - 2} \cdot {3}^{1} + {2}^{{2}^{n} - 3} \cdot {3}^{2} + \ldots + {2}^{{2}^{n - 1} + 1} \cdot {3}^{{2}^{n - 1} - 1} + {2}^{{2}^{n - 1}} \cdot {3}^{{2}^{n - 1}} \) ,而所有前项乘以 \( {3}^{{2}^{n - 1}} \) 将得到 \( {3}^{{2}^{n} - 1} + {3}^{{2}^{n} - 2} \cdot {2}^{1} + {3}^{{2}^{n} - 3} \cdot {2}^{2} + \ldots + {3}^{{2}^{n - 1} + 1} \cdot {2}^{{2}^{n - 1} - 1} + {3}^{{2}^{n - 1}} \cdot {2}^{{2}^{n - 1}} \) 。它们的和等于 \( {2}^{{2}^{n} - 1} + {2}^{{2}^{n} - 2} \cdot {3}^{1} + {2}^{{2}^{n} - 3} \cdot {3}^{2} + \ldots + {2}^{1} \cdot {3}^{{2}^{n} - 2} + {3}^{{2}^{n} - 1} \) ,因此证明完成。由于 \( \frac{{3}^{{2}^{n}} - {2}^{{2}^{n}}}{3 - 2} \) 等于 \( {2}^{{2}^{n} - 1} + {2}^{{2}^{n} - 2} \cdot {3}^{1} + {2}^{{2}^{n} - 3} \cdot {3}^{2} + \ldots + {2}^{1} \cdot {3}^{{2}^{n} - 2} + {3}^{{2}^{n} - 1} \) ,答案为 \( \frac{{3}^{{2}^{7}} - {2}^{{2}^{7}}}{3 - 2} = C \) 。-SmileKat32
解法4(工程师归纳法)
我们可以计算前几个部分积,并注意到 \( \mathop{\prod }\limits_{{n = 0}}^{{2}^{n}}\left( {{2}^{{2}^{n}} + {3}^{{2}^{n}}}\right) = {3}^{{2}^{n + 1}} - {2}^{{2}^{n + 1}} \) 。由于无需证明,
我们得到的产品是 \( {3}^{{2}^{7}} - {2}^{{2}^{7}} = {3}^{128} - {2}^{128} \) ,然后得意地点击了(C) \( {3}^{128} - {2}^{128} \) 。-rocketsri
解法5(平方差公式)
我们注意到第一项等于 \( {3}^{2} - {2}^{2} \) 。若将其乘以第二项,便得到 \( \left( {{3}^{2} - {2}^{2}}\right) \left( {{3}^{2} + {2}^{2}}\right) \) ,利用平方差公式可化简为 \( {3}^{4} - {2}^{4} \) 。再乘以第三项并再次使用平方差公式,得到 \( {3}^{8} - {2}^{8} \) 。依此继续,直到乘以最后一项 \( {3}^{64} + {2}^{64} \) ,最终得到 \( {3}^{128} - {2}^{128} \) 。
~数学少年100
2021年AMC 10A试题/第11题
问题
对于下列哪个整数 \( b \) ,以 \( b \) 为基数的数 \( {2021}_{b} - {221}_{b} \) 不能被3整除?
(A) 3 (B) 4 (C) 6 (D) 7 (E) 8
解决方案
我们有
\[ {2021}_{b} - {221}_{b} = {2000}_{b} - {200}_{b} = 2{b}^{3} - 2{b}^{2} = 2{b}^{2}\left( {b - 1}\right) . \]
该表达式可被3整除,除非 \( b \equiv 2{\;(\operatorname{mod}\;3)} \) 。唯一与2模3同余的选项是 \( |\mathbf{\left( E\right) }8 \) ~MRENTHUSIASM
2021年AMC 12A试题/第10题
以下题目同时出现在2021年AMC 10A第12题和2021年AMC 12A第10题,因此两道题均重定向至此页面。
问题
两个顶点朝下的正圆锥(right circular cones)如图示,装有等量液体。液面顶端的半径分别为3厘米和6厘米。向每个圆锥中投入一颗半径为1厘米的球形玻璃弹珠(marble),弹珠沉底并完全浸没,无液体溢出。求窄圆锥液面上升高度与宽圆锥液面上升高度之比。
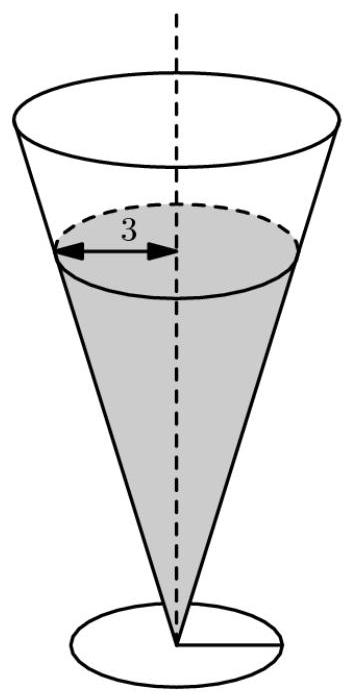
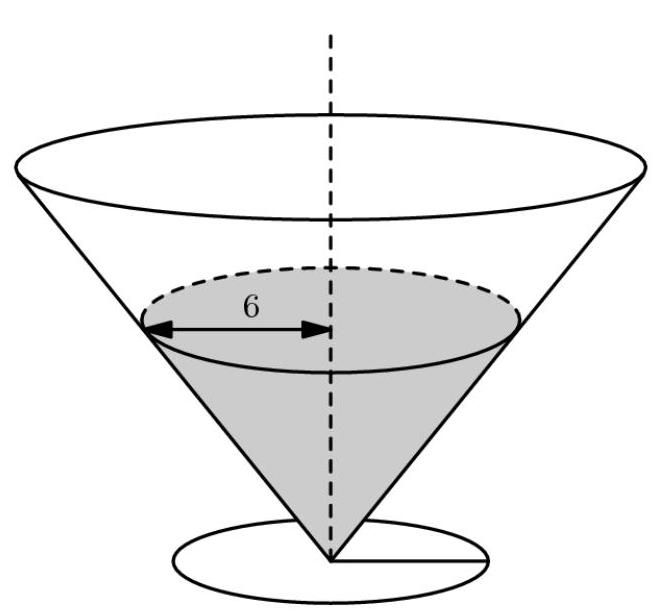
(A) \( 1 : 1 \) (B) \( {47} : {43} \) (C) \( 2 : 1 \) (D) \( {40} : {13} \)
解法1(用表格整理信息)
初始情境
底面半径 高度 体积
窄圆锥 \( \;3\;{h}_{1}\;\frac{1}{3}\pi {\left( 3\right) }^{2}{h}_{1} = {3\pi }{h}_{1} \)
宽圆锥 \( \;6\;{h}_{2}\;\frac{1}{3}\pi {\left( 6\right) }^{2}{h}_{2} = {12\pi }{h}_{2} \)
根据相似三角形:
对于窄圆锥,底面半径与高度之比为 \( \frac{3}{{h}_{1}} \) ,该比值保持不变。
对于宽圆锥,底面半径与高度之比为 \( \frac{6}{{h}_{2}} \) ,该比值保持不变。
令初始体积相等可得 \( {3\pi }{h}_{1} = {12\pi }{h}_{2} \) ,化简为 \( \frac{{h}_{1}}{{h}_{2}} = 4 \) 。
最终情境(由此产生两种解法)
解法1.1(分数技巧)
设窄圆锥与宽圆锥的底面半径分别为 \( {3x} \) 和 \( {6y}, \) ,其中 \( x, y > 1. \) ,得下表:
| 底边(Base) | 高(Height) | 体积(Volume) | |
| 窄圆锥(Narrow Cone) | \( {3x} \) | \( {h}_{1}x \) | \( \frac{1}{3}\pi {\left( 3x\right) }^{2}{h}_{1} = {3\pi }{h}_{1}{x}^{3} \) |
| 宽圆锥(Wide Cone) | \( {6y} \) | \( {h}_{2}y \) | \( \frac{1}{3}\pi {\left( 6y\right) }^{2}{h}_{2} = {12\pi }{h}_{2}{y}^{3} \) |
令最终体积相等,得到 \( {3\pi }{h}_{1}{x}^{3} = {12\pi }{h}_{2}{y}^{3}, \) ,化简为 \( {x}^{3} = {y}^{3}, \) 或 \( x = y. \)
最后,所求的比值为
\[ \frac{{h}_{1}x - {h}_{1}}{{h}_{2}y - {h}_{2}} = \frac{{h}_{1}\left( {x - 1}\right) }{{h}_{2}\left( {y - 1}\right) } = \frac{{h}_{1}}{{h}_{2}} = 1 \]
备注
- 本题使用了如下分数技巧:
对于不相等的正数 \( a, b, c \) 和 \( d \) ,若 \( \frac{a}{b} = \frac{c}{d} = k \) ,则 \( \frac{a \pm c}{b \pm d} = k \) 。
我们可以迅速证明这一结论:
由 \( \frac{a}{b} = \frac{c}{d} = k \) 可知 \( a = {bk} \) 且 \( c = {dk} \) 。因此,
\[ \frac{a \pm c}{b \pm d} = \frac{{bk} \pm {dk}}{b \pm d} = \frac{\left( {b \pm d}\right) k}{b \pm d} = k. \]
- 上述推导表明,无论投入固体的形状或体积如何,只要该固体沉底且完全浸没而不溢出液体,答案都不会改变。
~MRENTHUSIASM
解法1.2(暴力计算)
设窄锥与宽锥的底面半径分别为 \( {r}_{1} \) 和 \( {r}_{2}, \) 。
设窄锥与宽锥的液面上升高度分别为 \( \Delta {h}_{1} \) 和 \( \Delta {h}_{2}, \) 。我们有下表:
底面 高度 体积
\[ \text{Narrow Cone}\;{r}_{1}\;{h}_{1} + \Delta {h}_{1}\;\frac{1}{3}\pi {r}_{1}^{2}\left( {{h}_{1} + \Delta {h}_{1}}\right) \]
\[ \text{Wide Cone}\;{r}_{2}\;{h}_{2} + \Delta {h}_{2}\;\frac{1}{3}\pi {r}_{2}^{2}\left( {{h}_{2} + \Delta {h}_{2}}\right) \]
根据前述相似三角形,我们有
\[ \frac{3}{{h}_{1}} = \frac{{r}_{1}}{{h}_{1} + \Delta {h}_{1}} \Rightarrow {r}_{1} = \frac{3}{{h}_{1}}\left( {{h}_{1} + \Delta {h}_{1}}\right) \tag{1} \]
\[ \frac{6}{{h}_{2}} = \frac{{r}_{2}}{{h}_{2} + \Delta {h}_{2}} \Rightarrow {r}_{2} = \frac{6}{{h}_{2}}\left( {{h}_{2} + \Delta {h}_{2}}\right) \tag{2} \]
投入的大理石体积为 \( \frac{4}{3}\pi {\left( 1\right) }^{3} = \frac{4}{3}\pi \) 。现在为窄锥建立体积方程并解出 \( \Delta {h}_{1} \) :
\[ \frac{1}{3}\pi {r}_{1}^{2}\left( {{h}_{1} + \Delta {h}_{1}}\right) = {3\pi }{h}_{1} + \frac{4}{3}\pi \]
\[ \frac{1}{3}\pi \underset{\text{by }\left( 1\right) }{\underbrace{{\left( \frac{3}{{h}_{1}}\left( {h}_{1} + \Delta {h}_{1}\right) \right) }^{2}}}\left( {{h}_{1} + \Delta {h}_{1}}\right) = {3\pi }{h}_{1} + \frac{4}{3}\pi \]
\[ \frac{3}{{h}_{1}^{2}}{\left( {h}_{1} + \Delta {h}_{1}\right) }^{3} = 3{h}_{1} + \frac{4}{3} \]
\[ {\left( {h}_{1} + \Delta {h}_{1}\right) }^{3} = {h}_{1}^{3} + \frac{4{h}_{1}^{2}}{9} \]
\[ \Delta {h}_{1} = \sqrt[3]{{h}_{1}^{3} + \frac{4{h}_{1}^{2}}{9}} - {h}_{1}. \]
接着,为宽锥建立体积方程 \( \Delta {h}_{2} \) :
\[ \frac{1}{3}\pi {r}_{2}^{2}\left( {{h}_{2} + \Delta {h}_{2}}\right) = {12\pi }{h}_{2} + \frac{4}{3}\pi . \]
使用与上文完全相同的过程(但数字不同),我们得到
\[ \Delta {h}_{2} = \sqrt[3]{{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}} - {h}_{2}. \]
回忆 \( \frac{{h}_{1}}{{h}_{2}} = 4 \) 。因此,所求的比值为
\[ \frac{\Delta {h}_{1}}{\Delta {h}_{2}} = \frac{\sqrt[3]{{h}_{1}^{3} + \frac{4{h}_{1}^{2}}{9}} - {h}_{1}}{\sqrt[3]{{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}} - {h}_{2}} \]
\[ = \frac{\sqrt[3]{{\left( 4{h}_{2}\right) }^{3} + \frac{4{\left( 4{h}_{2}\right) }^{2}}{9}} - 4{h}_{2}}{\sqrt[3]{{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}} - {h}_{2}} \]
\[ = \frac{\sqrt[3]{{4}^{3}\left( {{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}}\right) } - 4{h}_{2}}{\sqrt[3]{{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}} - {h}_{2}} \]
\[ = \frac{4\sqrt[3]{{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}} - 4{h}_{2}}{\sqrt[3]{{h}_{2}^{3} + \frac{{h}_{2}^{2}}{9}} - {h}_{2}} \]
\[ = \text{(E)}4 : 1\text{.} \]
~MRENTHUSIASM
解法2(快速且粗略)
圆锥的高度未给出,因此假设高度非常大(即趋于无穷大),从而将圆锥近似为底面半径分别为3和6且高度无限大的圆柱。此时,较宽圆柱的底面积是较窄圆柱的4倍。由于向每个圆柱中投入体积相同的小球,较窄圆锥/圆柱中的水位应上升 \( \left| {\mathbf{E}\mathbf{b} - 4}\right| \) 倍。
-scrabbler94
解法3(更快更粗略)
由于一个的半径是另一个的两倍,且向两者投入面积相同的小球,答案可迅速得出。面积与半径的关系为 \( \frac{1}{4} \) ,此即答案。
2021 AMC 10A 试题/第13题
题目
边长分别为 \( {AB} = 2 \) 、 \( {AC} = 3 \) 、 \( {AD} = 4 \) 、 \( {BC} = \sqrt{13} \) 、 \( {BD} = 2\sqrt{5} \) 和 \( {CD} = 5 \) 的四面体 \( {ABCD} \) 的体积是多少?
(A) 3 (B) \( 2\sqrt{3} \) (C) 4 (D) \( 3\sqrt{3} \) (E) 6
解答
画出四面体并测试边长,我们发现三角形ABD和ABC均为直角三角形。现在利用棱锥体积公式计算四面体体积: \( \frac{3 \cdot 4 \cdot 2}{3 \cdot 2} = 4 \) ,因此答案为
2021 AMC 12A 试题/第12题
以下题目同时出现在2021 AMC 12A第12题和2021 AMC 10A第14题,因此两题均重定向至此页面。
问题
多项式 \( {z}^{6} - {10}{z}^{5} + A{z}^{4} + B{z}^{3} + C{z}^{2} + {Dz} + {16} \) 的所有根均为正整数,可重复。求 \( B \) 的值?
(A) -88 (B) -80 (C) -64 (D) -41 (E) -40
解法1:
根据韦达定理(Vieta's formulae),6个根之和为10,6个根之积为16。经观察,根为1, 1, 2, 2, 2, 2,因此函数为 \( {\left( z - \underline{1}\right) }^{2}{\left( z - \underline{2}\right) }^{4} = \left( {{z}^{2} - {2z} + 1}\right) \left( {{z}^{4} - 8{z}^{3} + {24}{z}^{2} - {32z} + {16}}\right) \) 。于是 \( B = - {32} - {48} - 8 = \left( \mathbf{A}\right) - {88}. \sim \) JHawk0224
解法2:
与解法1同法,得根为2,2,2,2,1,1。注意 \( B \) 为根的第3对称和(3rd symmetric sum)的相反数。对 \( \left( \begin{array}{l} 6 \\ 3 \end{array}\right) = {20} \) 个乘积 \( {r}_{a} \cdot {r}_{b} \cdot {r}_{c} \) 中1的个数进行分情况讨论,得 \( B = - \left( {\left( \begin{array}{l} 4 \\ 3 \end{array}\right) \left( \begin{array}{l} 2 \\ 0 \end{array}\right) \cdot {2}^{3} + \left( \begin{array}{l} 4 \\ 2 \end{array}\right) \left( \begin{array}{l} 2 \\ 1 \end{array}\right) \cdot {2}^{2} \cdot 1 + \left( \begin{array}{l} 4 \\ 1 \end{array}\right) \left( \begin{array}{l} 2 \\ 2 \end{array}\right) \cdot 2}\right) = - \left( {{32} + {48} + 8}\right) = {48} \) ~ ike.chen
2021 AMC 10A 第15题
问题
需从 \( \{ 1,2,3,4,5,6\} \) 中不重复地选取 \( A, B, C, \) 和 \( D \) 的值(即无两字母取值相同)。有多少种选法可使两曲线 \( y = A{x}^{2} + B \) 与 \( y = C{x}^{2} + D \) 相交?(曲线顺序无关;例如,选 \( A = 3, B = 2, C = 4, D = 1 \) 与选 \( A = 4, B = 1, C = 3, D = \) 视为相同)
(A) 30 (B) 60 (C) 90 (D) 180 (E) 360
解法1(直观):
将两曲线可视化,发现它们均为对称轴相同的抛物线。因顺序无关,设第一方程在第二方程之上,则 \( C > A \) 且 \( B > D \) 。故选四整数的方案数为 \( \left( \begin{array}{l} 6 \\ 2 \end{array}\right) \left( \begin{array}{l} 4 \\ 2 \end{array}\right) = {90} \) ,答案为 \( C \) 。~IceWolf10
解法2(代数):
设 \( y = A{x}^{2} + B = C{x}^{2} + D \) ,我们发现 \( A{x}^{2} - C{x}^{2} = {x}^{2}\left( {A - C}\right) = D - B \) ,因此由平凡不等式得 \( {x}^{2} = \frac{D - B}{A - C} \geq 0 \) 。这意味着 \( D - B \) 和 \( A - C \) 必须同为正或同为负。若分别为(A, C)和(B, D)选取两个不同的值,则有2种排列方式使分子与分母同为正/负(递增与递减)。然而最后必须除以2,因为这2条曲线不被视为不同。计算后得到
\[ \frac{1}{2} \cdot \left( \begin{array}{l} 6 \\ 2 \end{array}\right) \left( \begin{array}{l} 4 \\ 2 \end{array}\right) \cdot 2 = 0 \]
~ ike.chen
2021 AMC 12A 第16题
以下题目同时出现在2021 AMC 10A第16题和2021 AMC 12A第16题,因此两题均重定向至此页面
题目
在下列数列中,整数 \( n \) 在列表中出现 \( n \) 次,其中 \( 1 \leq n \leq {200} \) 。
\[ 1,2,2,3,3,3,4,4,4,4,\ldots ,{200},{200},\ldots ,{200} \]
该列表中所有数的中位数是多少?
(A) 100.5 (B) 134 (C) 142 (D) 150.5 (E) 167
解法1
总共有 \( 1 + 2 + .. + {199} + {200} = \frac{\left( {200}\right) \left( {201}\right) }{2} = {20100} \) 个数。设中位数为 \( k \) 。我们需要找到满足以下条件的中位数 \( k \) :
\[ \frac{k\left( {k + 1}\right) }{2} = {20100}/2, \]
或
\[ k\left( {k + 1}\right) = {20100} \]
注意 \( \sqrt{20100} \approx {142} \) 。将该值代入 \( k \) 得
\[ \frac{1}{2}\left( {142}\right) \left( {143}\right) = {10153}. \]
\( {10153} - {142} < {10050} \) ,因此142是第152和第153个数,故为所求答案。 \( \mathrm{\left( C\right) }{142} \)
注意可通过以下公式推导 \( \sqrt{20100} \approx {142} \) :
\[ \sqrt{n} = \sqrt{a + b} \approx \sqrt{a} + \frac{b}{2\sqrt{a} + 1}, \]
其中 \( a \) 为小于或等于 \( n \) 的完全平方数。我们取 \( a \) =19600,于是 \( \sqrt{a} = {140} \) ,且 \( b = {500} \) 。于是得到 \( n \approx {140} + \frac{500}{2\left( {140}\right) + 1} \approx {142} \) 。~ciceronii近似
解法2
该序列的第 \( x \) 个数通过二次公式(Quadratic Formula)得到 \( \left\lceil \frac{-1 \pm \sqrt{1 + {8x}}}{2}\right\rceil \) 。可以看到,若将 \( x \) 减半,我们得到 \( \left\lceil \frac{-1 \pm \sqrt{1 + {4x}}}{2}\right\rceil \) 。这大约等于该数除以 \( \sqrt{2} \cdot \frac{200}{\sqrt{2}} = {141.4} \) ,而142似乎是唯一接近的数,因此答案为 \( \left( C\right) {142} \sim \) Lopkiloinm
解法3(选项法)
我们先看选项 \( C \) ,即142。这意味着从1到142的数的数量大致等于从143到200的数的数量。
从1到142的数的数量为 \( \frac{{142}\left( {{142} + 1}\right) }{2} \) ,约10000;从143到200的数的数量为 \( \frac{{200}\left( {{200} + 1}\right) }{2} - \frac{{142}{\left( {142} + 1\right) }^{2}}{2} \) ,也约10000。因此,我们可以相当确定答案为 \( \left| {\left( C\right) {142}}\right| \)
-PureSwag
解法4
我们可以将数字按如下方式排列:

由于选项较为宽松,我们可以将其近似为一个等腰直角三角形,两腰长均为200。
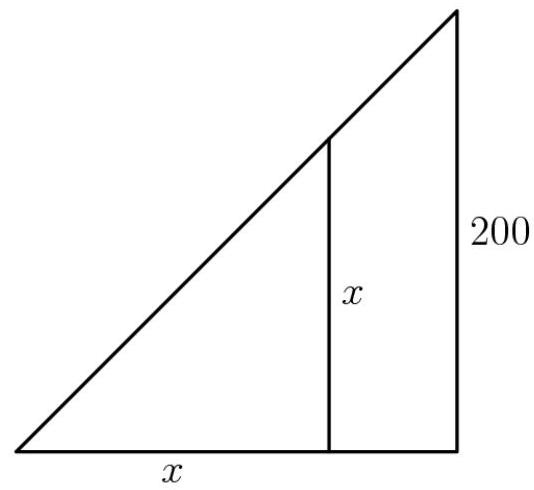
设 \( x \) 为边长,使得三角形两侧面积相等。则所求答案约为 \( x \) ,因为列表中大约一半的数字落在每一侧。
解得 \( x \) :
\[ \frac{{x}^{2}}{2} = \frac{1}{2} \cdot \frac{{200}^{2}}{2} \]
\[ {x}^{2} = \frac{1}{2} \cdot {200}^{2} \]
\[ x = \frac{200}{\sqrt{2}} = {100}\sqrt{2} \approx {141}. \]
我们发现 \( c \) (C)142最接近 \( x \) ,因此可以相当确定这就是答案。 \( \sim \) kxiang
2021 AMC 12A 第17题
以下题目同时出现在2021 AMC 10A第17题和2021 AMC 12A第17题,因此两题均重定向至此页
题目
梯形 \( {ABCD} \) 满足 \( \overline{AB} \parallel \overline{CD},{BC} = {CD} = {43} \) ,且 \( \overline{AD} \bot \overline{BD} \) 。设 \( O \) 为对角线 \( \overline{AC} \) 与 \( \overline{BD} \) 的交点, \( P \) 为 \( \overline{BD} \) 的中点。已知 \( {OP} = {11} \) ,则 \( {AD} \) 的长度可表示为 \( m\sqrt{n} \) ,其中 \( m \) 和 \( n \) 为正整数,且 \( n \) 不被任何素数的平方整除。求 \( m + n \) ?
(A) 65 (B) 132 (C) 157 (D) 194 (E) 215
图示
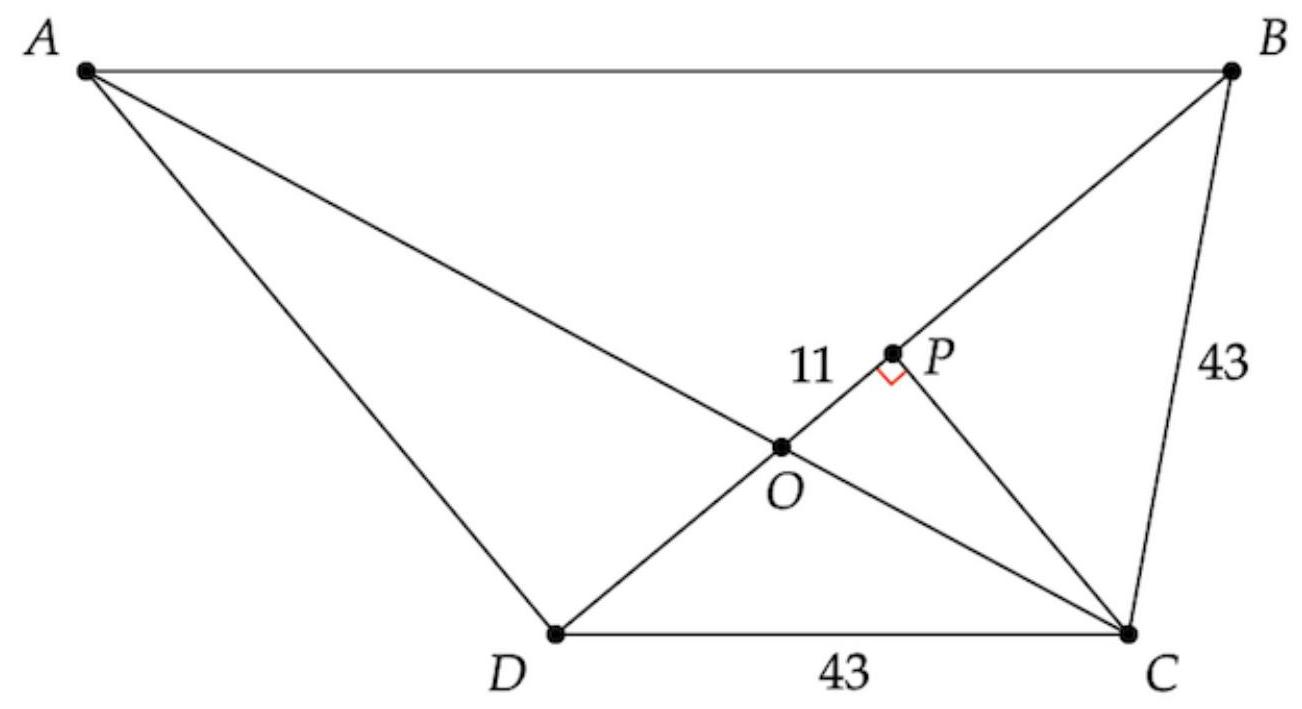
~MRENTHUSIASM(由 Geometry Expressions 提供)
解法 1
通过角度追踪可知 \( \bigtriangleup {BPC} \sim \bigtriangleup {BDA} \) ,因此
\[ 2 = \frac{BD}{BP} = \frac{AB}{BC} = \frac{AB}{43} \]
\[ {AB} = {86} \]
进一步的角度追踪表明 \( \bigtriangleup {ABO} \sim \bigtriangleup {CDO} \) ,因此
\[ 2 = \frac{AB}{CD} = \frac{BP}{PD} = \frac{\frac{BD}{2} + {11}}{\frac{BD}{2} - {11}} \]
\[ {BD} = {66} \]
由于 \( \bigtriangleup {ADB} \) 为直角,根据勾股定理可得
\[ {AD} = \sqrt{{86}^{2} - {66}^{2}} \]
\[ {AD} = 4\sqrt{190} \]
\[ 4\sqrt{190} \Rightarrow 4 + {190} = \text{D) 194} \]
https://artofproblemsolving.com/wiki/index.php/2021_AMC_12A_Problems/Problem_17
~mn28407
解法 2(一对相似三角形,再求面积)
因为 \( \bigtriangleup {BCD} \) 是以 \( \overline{CB} \) 和 \( \overline{CD}, \) 为腰的等腰三角形,所以中线 \( \overline{CP} \) 也是 \( \bigtriangleup {BCD}. \) 的高。设 \( {DO} = x \) 和 \( {CP} = h \) ,我们有 \( {PB} = x + {11} \) 。
由于 \( \bigtriangleup {ADO} \sim \bigtriangleup {CPO} \) 由 AA 相似,我们有
\[ {AD} = {CP} \cdot \frac{DO}{PO} = h \cdot \frac{x}{11}. \]
用方括号表示面积。注意到 \( \left\lbrack {ADO}\right\rbrack = \left\lbrack {BCO}\right\rbrack \) (根据同底等高, \( \left\lbrack {ADC}\right\rbrack = \left\lbrack {BCD}\right\rbrack . \)
两边同时减去 \( \left\lbrack {OCD}\right\rbrack \) 得 \( \left\lbrack {ADO}\right\rbrack = \left\lbrack {BCO}\right\rbrack \) 。)。两边同乘以 2,我们得到
\[ 2\left\lbrack {ADO}\right\rbrack = 2\left\lbrack {BCO}\right\rbrack \]
\[ \frac{{x}^{2}h}{11} = \left( {x + {22}}\right) h \]
\[ {x}^{2} = {11x} + {11} \cdot {22} \]
\[ \left( {x - {22}}\right) \left( {x + {11}}\right) = 0 \]
\[ x = {22}\text{.} \]
在 \( \bigtriangleup {CPB}, \) 中,我们有
\[ h = \sqrt{{43}^{2} - {33}^{2}} = \sqrt{{76} \cdot {10}} = 2\sqrt{190} \]
且
\[ {AD} = h \cdot \frac{x}{11} = 4\sqrt{190}. \]
最终, \( 4 + {190} = \left( \begin{array}{l} \mathbf{D} \end{array}\right) {194} \) ~MRENTHUSIASM
解法 3(简版)
设 \( {CP} = y \) 且 \( {CP} \) 为 \( {DB} \) 的垂直平分线。设 \( {DO} = x, \) ,则 \( {DP} = {PB} = {11} + x. \)
(1) \( \bigtriangleup {CPO} \sim \bigtriangleup {ADO} \) ,于是得到 \( \frac{AD}{x} = \frac{y}{11} \) ,或 \( {AD} = \frac{xy}{11} \) 。
(2) 在 \( \bigtriangleup {CDP} \) 上应用勾股定理得到 \( {\left( {11} + x\right) }^{2} + {y}^{2} = {43}^{2} \) 。
(3) \( \bigtriangleup {BPC} \sim \bigtriangleup {BDA} \) 的比例为 \( 1 : 2 \) ,因此 \( {AD} = {2y} \) 。
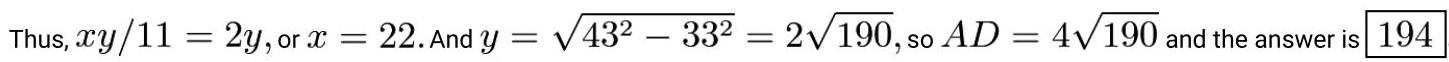
解法4——延长直线
注意到 \( \bigtriangleup {BPC} \) 与 \( \bigtriangleup {DPC} \) 全等;二者均与 \( \bigtriangleup {BDA} \) 相似。我们将 \( \overline{AD} \) 和 \( \overline{BC} \) 分别延长,越过点 \( D \) 和 \( C \) ,使它们交于点 \( E \) 。观察到 \( \angle {BDE} \) 为90度,且 \( \angle {DBE} \cong \angle {PBC} \cong \angle {DBA} \Longrightarrow \angle {DBE} \cong \angle {DBA} \) 。因此,由角边角(ASA)可知
\( \bigtriangleup {ABD} \cong \bigtriangleup {EBD} \) ,因此 \( {AD} = {ED} \) ,这意味着 \( D \) 是 \( {AE} \) 的中点。设 \( M \) 为 \( \overline{DE} \) 的中点。注意 \( \bigtriangleup {CME} \) 与 \( \bigtriangleup {BPC} \) 全等,因此 \( {BC} = {CE} \) ,这意味着 \( C \) 是 \( \overline{BE} \) 的中点。
因此, \( \overline{AC} \) 和 \( \overline{BD} \) 都是 \( \bigtriangleup {ABE} \) 的中线。这意味着 \( O \) 是 \( \bigtriangleup {ABE} \) 的重心;因此,由于重心将中线分为2:1的比例, \( \frac{BO}{2} = {DO} = \frac{BD}{3} \) 。回忆 \( P \) 是 \( {BD} \) 的中点; \( {DP} = \frac{BD}{2} \) 。题目告诉我们 \( {OP} = {11} \) ; \( {DP} - {DO} = {11} \) ;我们可以用 \( {DB} \) 表示:
https://artofproblemsolving.com/wiki/index.php/2021_AMC_12A_Problems/Problem_17
2021/3/7
\[ \frac{DB}{2} - \frac{DB}{3} = \frac{DB}{6} = {11} \Rightarrow {DB} = {66}. \]
我们即将完成。 \( \bigtriangleup {ABD} \) 的每条边长都是对应边 \( \bigtriangleup {CBP} \) 或 \( \bigtriangleup {CPD} \) 的两倍,因为这些三角形相似;这意味着 \( {AB} = 2 \cdot {43} = {86} \) 。现在,对 \( \bigtriangleup {ABD} \) 应用勾股定理, \( A{B}^{2} - B{D}^{2} = A{D}^{2}\;\Longrightarrow \;{86}^{2} - {66}^{2} = A{D}^{2}\;\Longrightarrow \;{AD} = \sqrt{3040}\;\Longrightarrow \;{AD} = 4\sqrt{190}. \) \( 4 + {190} = {194},\mathbf{D} \)
2021 AMC 12A 第18题
以下题目同时出现在2021 AMC 10A第18题和2021 AMC 12A第18题,因此两题均重定向至此页面
题目
设 \( f \) 为定义在正有理数集合上的函数,满足对所有正有理数 \( a \) 和 \( b \) 都有 \( f\left( {a \cdot b}\right) = f\left( a\right) + f\left( b\right) \) 。进一步假设 \( f \) 还具有性质:对每个素数 \( p \) 都有 \( f\left( p\right) = p \) 。对于下列哪个数 \( x \) ,有 \( f\left( x\right) < 0 \) ?
(A) \( \frac{17}{32} \) (B) \( \frac{11}{16} \) (C) \( \frac{7}{9} \) (D) \( \frac{7}{6} \) (E) \( \frac{25}{11} \) 解法1 浏览各解法可见 \( f\left( \frac{25}{11}\right) \) 可表示为 \( f\left( {\frac{25}{11} \cdot {11}}\right) = f\left( {11}\right) + f\left( \frac{25}{11}\right) \) ,因此利用素数拼凑可得 \( {10} = {11} + f\left( \frac{25}{11}\right) \) ,于是 \( f\left( \frac{25}{11}\right) = - 1 \) 或 \( E \) 。
-Lemonie
\[ f\left( {\frac{25}{11} \cdot {11}}\right) = f\left( {25}\right) = f\left( 5\right) + f\left( 5\right) = {10} \]
- awesomediabrine
解法2
我们知道 \( f\left( p\right) = f\left( {p \cdot 1}\right) = f\left( p\right) + f\left( 1\right) \) 。由传递性,我们有
\[ f\left( p\right) = f\left( p\right) + f\left( 1\right) . \]
两边减去 \( f\left( p\right) \) 得 \( 0 = f\left( 1\right) \) 。同时
\[ f\left( 2\right) + f\left( \frac{1}{2}\right) = f\left( 1\right) = 0 \Rightarrow 2 + f\left( \frac{1}{2}\right) = 0 \Rightarrow f\left( \frac{1}{2}\right) = - 2 \]
\[ f\left( 3\right) + f\left( \frac{1}{3}\right) = f\left( 1\right) = 0 \Rightarrow 3 + f\left( \frac{1}{3}\right) = 0 \Rightarrow f\left( \frac{1}{3}\right) = - 3 \]
\[ f\left( {11}\right) + f\left( \frac{1}{11}\right) = f\left( 1\right) = 0 \Rightarrow {11} + f\left( \frac{1}{11}\right) = 0 \Rightarrow f\left( \frac{1}{11}\right) = - {11} \]
\[ \text{In}\left( \mathbf{A}\right) \text{we have}f\left( \frac{17}{32}\right) = {17} + {5f}\left( \frac{1}{2}\right) = {17} - 5\left( 2\right) = 7\text{.} \]
\[ \text{In}\left( \mathbf{B}\right) \text{we have}f\left( \frac{11}{16}\right) = {11} + {4f}\left( \frac{1}{2}\right) = {11} - 4\left( 2\right) = 3\text{.} \]
\[ \text{In}\left( \mathbf{C}\right) \text{we have}f\left( \frac{7}{9}\right) = 7 + {2f}\left( \frac{1}{3}\right) = 7 - 2\left( 3\right) = 1\text{.} \]
\[ \text{In}\left( \mathbf{D}\right) \text{we have}f\left( \frac{7}{6}\right) = 7 + f\left( \frac{1}{2}\right) + f\left( \frac{1}{3}\right) = 7 - 2 - 3 = 2\text{.} \]
\[ \text{In}\left( \mathbf{E}\right) \text{we have}f\left( \frac{25}{11}\right) = {10} + f\left( \frac{1}{11}\right) = {10} - {11} = - 1\text{.} \]
https://artofproblemsolving.com/wiki/index.php/2021_AMC_12A_Problems/Problem_18
2021/3/7
因此,答案为(E) \( \frac{25}{11} \)
~JHawk0224 ~awesomediabrine
解法3(深入)
考虑有理数 \( \frac{a}{b} \) ,其中 \( a, b \) 为整数。我们有 \( f\left( a\right) = f\left( {\frac{a}{b} \cdot b}\right) = f\left( \frac{a}{b}\right) + f\left( b\right) \) 。于是 \( f\left( \frac{a}{b}\right) = f\left( a\right) - f\left( b\right) \) 。设 \( p \) 为素数。注意到 \( f\left( {p}^{k}\right) = {kf}\left( p\right) \) 。且 \( f\left( p\right) = p \) 。因此若 \( a = {p}_{1}^{{a}_{1}}{p}_{2}^{{a}_{2}}\cdots {p}_{k}^{{a}_{i}} \) ,则 \( f\left( a\right) = {a}_{1}{p}_{1} + {a}_{2}{p}_{2} + .... + {a}_{k}{p}_{k} \) 。我们只需使其大于 \( f\left( b\right) \) 。注意到在选项 \( A, B, C, \) 和 \( D \) 中,分子(a)的素因子少于分母,因此它们更不可能成立。我们先检验 \( E \) ,其成立,故答案为 \( \mathbf{\left( E\right) } \)
~yofro
解法4(极为全面,与解法3类似)
结果
我们得到以下重要结果:
(1) 对所有正有理数 \( {a}_{k} \) 和正整数 \( n \) ,有 \( f\left( {\mathop{\prod }\limits_{{k = 1}}^{n}{a}_{k}}\right) = \mathop{\sum }\limits_{{k = 1}}^{n}f\left( {a}_{k}\right) \)
(2) \( f\left( {a}^{n}\right) = {nf}\left( a\right) \) 对所有正有理数 \( a \) 和正整数 \( n \) 成立
(3) \( f\left( 1\right) = 0 \)
(4) \( f\left( \frac{1}{a}\right) = - f\left( a\right) \) 对所有正有理数 \( a \) 成立
~MRENTHUSIASM
证明
结果(1)可通过归纳法证明。
结果 \( \left( 2\right) : \) 由于正整数次幂只是底数的重复乘法,我们将用结果(1)来证明结果 \( \left( 2\right) : \)
\[ f\left( {a}^{n}\right) = f\left( {\mathop{\prod }\limits_{{k = 1}}^{n}a}\right) = \mathop{\sum }\limits_{{k = 1}}^{n}f\left( a\right) = {nf}\left( a\right) . \]
结果 \( \left( 3\right) : \) 对所有正有理数 \( a, \) 我们有
\[ f\left( a\right) = f\left( {a \cdot 1}\right) = f\left( a\right) + f\left( 1\right) . \]
因此,我们得到 \( f\left( 1\right) = 0, \) 从而结果(3)成立。
结果 \( \left( 4\right) : \) 对所有正有理数 \( a, \) 我们有
\[ f\left( a\right) + f\left( \frac{1}{a}\right) = f\left( {a \cdot \frac{1}{a}}\right) = f\left( 1\right) = 0. \]
由此可得 \( f\left( \frac{1}{a}\right) = - f\left( a\right) \) ,且结果(4)成立。
~MRENTHUSIASM
解答
2021/3/7
对所有正整数 \( x \) 和 \( y \) ,设 \( \mathop{\prod }\limits_{{k = 1}}^{m}{p}_{k}^{{e}_{k}} \) 和 \( \mathop{\prod }\limits_{{k = 1}}^{n}{q}_{k}^{{d}_{k}} \) 分别为它们的素因数分解,我们有
\[ f\left( \frac{x}{y}\right) = f\left( x\right) + f\left( \frac{1}{y}\right) \]
\[ = f\left( x\right) - f\left( y\right) \]
\[ = f\left( {\mathop{\prod }\limits_{{k = 1}}^{m}{p}_{k}^{{e}_{k}}}\right) - f\left( {\mathop{\prod }\limits_{{k = 1}}^{n}{q}_{k}^{{d}_{k}}}\right) \]
\[ = \left\lbrack {\mathop{\sum }\limits_{{k = 1}}^{m}f\left( {p}_{k}^{{e}_{k}}\right) }\right\rbrack - \left\lbrack {\mathop{\sum }\limits_{{k = 1}}^{n}f\left( {q}_{k}^{{d}_{k}}\right) }\right\rbrack \]
\[ = \left\lbrack {\mathop{\sum }\limits_{{k = 1}}^{m}{e}_{k}f\left( {p}_{k}\right) }\right\rbrack - \left\lbrack {\mathop{\sum }\limits_{{k = 1}}^{n}{d}_{k}f\left( {q}_{k}\right) }\right\rbrack \]
\[ = \left\lbrack {\mathop{\sum }\limits_{{k = 1}}^{m}{e}_{k}{p}_{k}}\right\rbrack - \left\lbrack {\mathop{\sum }\limits_{{k = 1}}^{n}{d}_{k}{q}_{k}}\right\rbrack . \]
我们对每个选项中的分数应用函数 \( f \) :
(A) \( f\left( \frac{17}{32}\right) = f\left( \frac{{17}^{1}}{{2}^{5}}\right) = \left\lbrack {1\left( {17}\right) }\right\rbrack - \left\lbrack {5\left( 2\right) }\right\rbrack = 7 \)
(B) \( f\left( \frac{11}{16}\right) = f\left( \frac{{11}^{1}}{{2}^{4}}\right) = \left\lbrack {1\left( {11}\right) }\right\rbrack - \left\lbrack {4\left( 2\right) }\right\rbrack = 3 \)
(C) \( f\left( \frac{7}{9}\right) = f\left( \frac{{7}^{1}}{{3}^{2}}\right) = \left\lbrack {1\left( 7\right) }\right\rbrack - \left\lbrack {2\left( 3\right) }\right\rbrack = 1 \)
(D) \( f\left( \frac{7}{6}\right) = f\left( \frac{{7}^{1}}{{2}^{1} \cdot {3}^{1}}\right) = \left\lbrack {1\left( 7\right) }\right\rbrack - \left\lbrack {1\left( 2\right) + 1\left( 3\right) }\right\rbrack = 2 \)
(E) \( f\left( \frac{25}{11}\right) = f\left( \frac{{5}^{2}}{{11}^{1}}\right) = \left\lbrack {2\left( 5\right) }\right\rbrack - \left\lbrack {1\left( {11}\right) }\right\rbrack = - 1 \)
因此,答案为 \( \left( {\mathbf{E}\text{ }}\right) \frac{25}{11} \) 。
~MRENTHUSIASM
解法5
题目给出f(p)=p。若令a=p、b=1,则得f(p)=f(p)+f(1),从而推出f(1)=0。注意到所有选项都是分数,这意味着我们必须用整数乘以分数才能求解。因此,尝试代入分数并求解。若代入a=p、b=1/p,则得f(1)=f(p)+f(1/p)。可解得f(1/p)=-f(p)!这提供了所需信息。逐一验证选项,最终答案为E。
2021 AMC 10A 第19题
题目
由以下图形所围成区域的面积为
\[ {x}^{2} + {y}^{2} = 3\left| {x - y}\right| + 3\left| {x + y}\right| \]
是 \( m + {n\pi } \) ,其中 \( m \) 和 \( n \) 为整数。 \( m + n \) 的值是多少?
(A) 18 (B) 27 (C) 36 (D) 45 (E) 54
解法1
为攻克此题,需分情况讨论:
情况1: \( \left| {x - y}\right| = x - y,\left| {x + y}\right| = x + y \)
代入并化简得 \( {x}^{2} - {6x} + {y}^{2} = 0 \) ,即 \( {\left( x - 3\right) }^{2} + {y}^{2} = {3}^{2} \) ,得到一个以(3,0)为圆心、半径为3的圆。
\[ \text{Case 2:}\left| {x - y}\right| = y - x,\left| {x + y}\right| = x + y \]
再次代入并化简得 \( {x}^{2} + {y}^{2} - {6y} = 0 \) ,即 \( {x}^{2} + {\left( y - 3\right) }^{2} = {3}^{2} \) 。得到一个以(0,3)为圆心、半径为3的圆。
\[ \text{Case 3:}\left| {x - y}\right| = x - y,\left| {x + y}\right| = - x - y \]
重复上述过程得 \( {x}^{2} + {y}^{2} + {6y} = 0 \) ,即 \( {x}^{2} + {\left( y + 3\right) }^{2} = {3}^{2} \) 。得到一个以(0,-3)为圆心、半径为3的圆。
情况4: \( \left| {x - y}\right| = y - x,\left| {x + y}\right| = - x - y \)
最后一次:得 \( {x}^{2} + {y}^{2} + {6x} = 0 \) ,即 \( {\left( x + 3\right) }^{2} + {y}^{2} = {3}^{2} \) 。得到一个以(-3,0)为圆心、半径为3的圆。
综合所有情况并在笛卡尔平面上绘制后,图形如下:
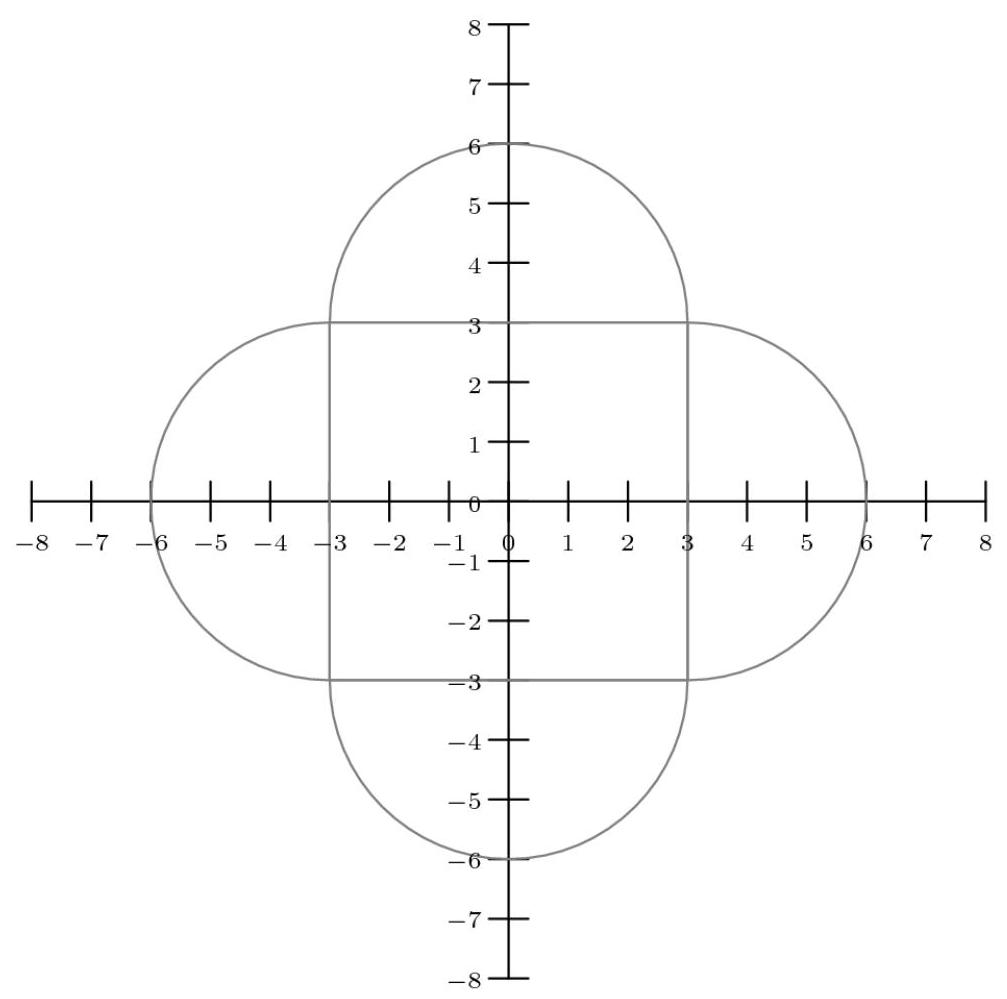
现在,阴影区域是一个边长为6的正方形,四角各有一个半径为3的半圆。其面积为 \( 6 \cdot 6 + 4 \cdot \frac{9\pi }{2} = {36} + {18\pi } \) 。答案是 \( {36} + {18} \) ,由Bryguy提供解答
2021 AMC 10A 第20题
题目
将序列1,2,3,4,5重新排列,使得没有三个连续项递增,也没有三个连续项递减,共有多少种方式?
(A) 10 (B) 18 (C) 24 (D) 32 (E) 44
解法1(暴力枚举)
我们列出全部120种情况。以下这些情况是满足条件的:
13254,14253,14352,15243,15342,21435,21534,23154,24153,24351,25143,25341,
31425,31524,32415,32451,34152,34251,35142,35241,41325,41523,42315,42513,
43512, 45132, 45231, 51324, 51423, 52314, 52413, 53412.We count
筛选后得到 \( \mathrm{D} : {32} \) 种有效排列。~contactbibliophile
解法2(分类讨论)
从左到右阅读各项,我们有两种情况:
情况 \( \# 1 : + , - , + , - \)
情况 \( \# 2 : - , + , - , + \)
(十表示递增,-表示递减。)
对于情况 \( \# 1, \) ,注意第二项和第四项中必须有一个是5,另一个必须是3或4。我们有四个子情况:
(1) \( \_ 3\_ 5 \) _____
(2) \( \_ 5\_ 3 \) _____
(3) _4_5_
(4) _5_4_
对于 \( \left( 1\right) , \) ,前两个空位必须是1和2的某种顺序,最后一个空位必须是4,共2种可能。同理,(2)也有2种可能。
对于 \( \left( 3\right) , \) ,数字1、2、3无限制,因此有 \( 3! = 6 \) 种可能。同理,(4)也有6种可能。
合在一起, \( \mathrm{{Case}}\# 1 \) 有 \( 2 + 2 + 6 + 6 = {16} \) 种可能。由于对称性, \( \mathrm{{Case}}\# 2 \) 也有16种可能。合在一起,答案是 \( {16} + {16} = 0 \) (D) 32。
这道题与2004年AIME I第6题有些相似:
https://artofproblemsolving.com/wiki/index.php/2004_AIME_I_Problems/Problem_6
~MRENTHUSIASM
解法3(与解法2类似)
与解法2一样,我们分两种情况。由于对称性,只需计算其中一种情况。在本解法中,我们将处理 \( - , + , - , + \) 。不是从5开始,而是从1开始。
放置1有两种方式:
_1
_____1_
接下来放置2,它可以紧挨1并在外侧,也可以放在另一种情况下1会放的位置。于是我们现在有
另外两个“子情况”:2021/3/7
_1_2_(情况1)
21_____(情况2)
对于情况1,其余数字有3!种排列方式,因为没有限制。
对于情况2,我们需要考虑将3、4、5按a>b 现在我们得到结果,乘以2(对称性),再乘以2(1的放置方式),再乘以(3!+2!)(2的两种不同放置情况),得到 \( 2 * 2 * \left( {3! + 2!}\right) = 4 * \left( {6 + 2}\right) = {32} \) 。 ~~Xhte解法4:对称性
我们只需计算当5是第4位和第5位时的重排数。求出总数后乘以2,再加上5是第3位的情况即可得到答案。
情况1:5是第5位。_____
那么4只能是第1位或第3位。
4 _____ 5,则唯一可能是3在第3位,因此可以是231或132,共2种结果。
_____4 _____ 5,则第1位必须是2或3;2有1种方式,3有2种方式。(不能是1,否则首位递增)。因此4在中间且5在最后共有3种方式。
情况2:5是第4位。_____ 5 _____
那么最后一位可以是4个数字1、2、3、4中的任意一个。假设最后一位是4,那么第二位应取剩余数字中最大的,以避免递增或递减顺序。剩下的两个数字可以互换,共有 \( 2! \) 种方式。4种情况都可行,因此情况2共有 \( 2! + 2! + 2! + 2! = 8 \) 种方式。
情况 \( 3:5 \) 在中间。_____5_____
于是只有两种情形:1.42513,此时4和3可互换,共 \( 2! * 2! \) 种;或者43512,此时4和2可互换,但不能是23514,因此只有2种可能:43512,21534。
因此,情况3共有 \( 4 + 2 = 6 \) 种方式。
\( 8 + 3 + 2 = {13} \) ,所以情况1和情况2在同时考虑递增与递减时的总方式数为 \( {13} * 2 = {26} \) 。
\[ {26} + 6 = 0\text{D)}{32}\text{.} \]
~Michael595
2021 AMC 10A 问题/第21题
问题
设 \( {ABCDEF} \) 为一个等角六边形。直线 \( {AB},{CD}, \) 与 \( {EF} \) 围成的三角形面积为 \( {192}\sqrt{3} \) ,直线 \( {BC},{DE}, \) 与 \( {FA} \) 围成的三角形面积为 \( {324}\sqrt{3} \) 。六边形 \( {ABCDEF} \) 的周长可表示为 \( m + n\sqrt{p} \) ,其中 \( m, n, \) 和 \( p \) 为正整数,且 \( p \) 不被任何素数的平方整除。求 \( m + n + p \) ?
(A) 47 (B) 52 (C) 55 (D) 58 (E) 63
解法(题目错位?)
注意,给定直线的延长线将围成一个等边三角形,因为六边形是等角的。第一个三角形面积为 \( {192}\sqrt{3} \) ,故其边长为 \( \sqrt{{192} \cdot 4} = {16}\sqrt{3} \) ;第二个三角形面积为 \( {324}\sqrt{3} \) ,故其边长为 \( \sqrt{4 \cdot {324}} = {36} \) 。通过用同一等边三角形的不同边替换某些长度,可将第一个值设为 \( {AB} + {CD} + {EF} \) ,第二个值设为 \( {BC} + {DE} + {FA} \) 。六边形的周长即为二者之和,即 \( {16}\sqrt{3} + {36} \) 和 \( {16} + 3 + {36} = {55} \) (C)
OmegaLearn 视频解法(角追踪与等边三角形)
https://youtu.be/ptBwDcmDaLA
~pi_is_3.14
2021 AMC 10A 问题/第22题
问题
希兰(Hiram)的代数笔记共有50页,打印在25张纸上;第一张纸包含第1页和第2页,第二张纸包含第3页和第4页,依此类推。一天,他把笔记放在桌上后去吃午饭,室友决定从笔记中间借走几页。希兰回来后,发现室友取走了连续若干张纸,且所有剩余纸张上的页码平均值(算术平均数)恰好为19。问借走了多少张纸?
(A) 10 (B) 13 (C) 15 (D) 17 (E) 20
解答
假设室友取走了第 \( a \) 页到第 \( b \) 页,即页码 \( {2a} - 1 \) 到 \( {2b} \) 。由于共取走了 \( \left( {{2b} - {2a} + 2}\right) \) 个页码,
\( \frac{\left( {{2a} - 1 + {2b}}\right) \left( {{2b} - {2a} + 2}\right) }{2} + {19}\left( {{50} - \left( {{2b} - {2a} + 2}\right) }\right) = \frac{{50} * {51}}{2} \Rightarrow \left( {{2a} + {2b} - {39}}\right) \left( {b - a + 1}\right) = \frac{{50} * {13}}{2} = {25} * {13} \) .
首先想到的可能解是
\( {2a} + {2b} - {39} = {25}, b - a + 1 = {13} \Longrightarrow a + b = {32}, b - a = {12} \) ,这确实成立,得到 \( b = {22} \) 和 \( a = {10} \) 。答案为 \( {22} - {10} + 1 = \left( {\mathbf{B}/{13}}\right) \) ~LCZ
解法2(变量选择不同,逻辑类似)
设被移除的最小页码为 \( k, \) ,共移除了 \( n \) 页,则被移除的最大页码为 \( k + n - 1 \) 。
备注:
- 移除 \( n \) 页意味着移除了 \( \frac{n}{2} \) 张纸,因此 \( n \) 必须为偶数。
- \( k \) 必须为奇数,因为被移除的最小页码位于右侧(奇数页)。
- \( 1 + 2 + 3 + \cdots + {50} = \frac{{51}\left( {50}\right) }{2} = {1275} \) .
- 被移除的页码之和为 \( \frac{\left( {{2k} + n - 1}\right) n}{2} \) 。
综上,我们有
\[ \frac{{1275} - \frac{\left( {{2k} + n - 1}\right) n}{2}}{{50} - n} = {19} \]
\[ {1275} - \frac{\left( {{2k} + n - 1}\right) n}{2} = {19}\left( {{50} - n}\right) \]
\[ {2550} - \left( {{2k} + n - 1}\right) n = {38}\left( {{50} - n}\right) \]
\[ {2550} - \left( {{2k} + n - 1}\right) n = {1900} - {38n} \]
\[ {650} = \left( {{2k} + n - {39}}\right) n\text{.} \]
650的因数为
\[ 1,2,5,{10},{13},{25},{26},{50},{65},{130},{325},{650}\text{.} \]
由于 \( n \) 为偶数,我们只需考虑少数几种情况:
| \( n \) | \( {2k} + n - {39} \) | \( k \) |
| 2 | 325 | 181 |
| 10 | 65 | 47 |
| 26 | 25 | 19 |
| 50 | 13 | 1 |
| 130 | 5 | 阴性 |
| 650 | 1 | 阴性 |
由于 \( 1 \leq k \leq {50}, \) 只有 \( k = {47},{19},1 \) 是可能的:
如果 \( k = {47}, \) ,那么从第47页开始取10页,笔记页将用完。
如果 \( k = 1, \) ,那么剩余页的平均页码将无定义,因为(从第1页开始取50页后)没有剩余页。

解法3
设 \( n \) 为借出的张数,其平均页码为 \( k + {25.5} \) 。剩余的 \( {25} - n \) 张平均页码为19,低于全部50页的平均页码25.5,因此 \( k > 0 \) 。由于借出的张从奇数页开始、偶数页结束,我们有 \( k \in \mathbb{N} \) 。我们注意到 \( n < {25} \) 和 \( k \leq \left( {{49} + {50}}\right) /2 - {25.5} = {24} < {25} \) 。
平均页码从25.5加权增加到 \( k + {25.5} \) ,应等于从25.5加权减少到19,权重为每组页数(借出 vs. 剩余),因此
\[ {2nk} = 2\left( {{25} - n}\right) \left( {{25.5} - {19}}\right) = {13}\left( {{25} - n}\right) \Rightarrow {13} \mid n\text{ or }{13} \mid k \]
由于 \( n, k < {25} \) ,我们得到 \( n = {13} \) 或 \( k = {13} \) 。若 \( n = {13} \) ,则 \( k = 6 \) 。若 \( k = {13} \) ,则 \( {2n} = {25} - n \) ,这不可能。因此答案应为 \( n = \) (B) 13
2021 AMC 12A 试题/第23题
以下题目同时出现在2021 AMC 10A第23题和2021 AMC 12A第23题,因此两题均重定向至此页。
题目
青蛙弗里达在一个 \( 3 \times 3 \) 的方格网格上开始一系列跳跃,每次跳一格,并随机选择方向——上、下、左或右。她不斜跳。若某次跳跃方向会使弗里达跳出网格,她会“绕回”跳到对边。例如,若弗里达从中心格开始,连续两次向上跳,第一次跳到顶行中间格,第二次则绕回到底行中间格。假设弗里达从中心格出发,最多随机跳四次,并在第一次落到角格时停止。求她在四次跳跃内到达角格的概率。
(A) \( \frac{9}{16} \) (B) \( \frac{5}{8} \) (C) \( \frac{3}{4} \) (D) \( \frac{25}{32} \) (E) \( \frac{13}{16} \)
解法1(补集计数)
我们将使用补集计数。首先,青蛙向左跳的概率为 \( \frac{1}{4} \) 。我们观察到对称性,因此最终答案将
乘以4(对应4个方向),且由于 \( 4 \cdot \frac{1}{4} = 1 \) ,我们将忽略前面的概率。
从左侧开始,她要么向左走到另一条边 \( \left( \frac{1}{4}\right) \) ,要么回到中心 \( \left( \frac{1}{4}\right) \) 。是时候分情况讨论了。
情况1:她回到中心。
现在,她可以朝任意4个方向移动,然后从该边缘又有2种选择。这给出了 \( \frac{1}{2} \) 。——情况1结束
情况2:她走向另一条边(最右侧)。
子情况1:她回到左边缘。她现在有两个去处,即 \( \frac{1}{2} \)
子情况2:她前往中心。现在任何一步都行得通。
\( \frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot 1 = \frac{1}{8} + \frac{1}{4} = \frac{3}{8} \) 针对本案例。——案例2结束
她以概率 \( \frac{1}{4} \) 返回情况1的中心,并以概率 \( \frac{1}{4} \) 返回右边缘
因此,我们的答案是 \( \frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{3}{8} = \frac{1}{4}\left( {\frac{1}{2} + \frac{3}{8}}\right) = \frac{1}{4} \cdot \frac{7}{8} = \frac{7}{32} \)
但别忘了使用补集计数(complementary counting)。于是,我们得到 \( 1 - \frac{7}{32} = \frac{25}{32} \Rightarrow D \) 、 \( D \) 、 \( \sim \) firebolt360
喜欢视频讲解的同学请看:https://youtu.be/ude2rz01cmk ~ firebolt360
解法2(直接计数与概率状态)
我们可以画一个包含三种状态的状态图:中心(center)、边缘(edge)和角落(corner)。用M表示中心,E表示边缘,C表示角落。Frieda在不超过四步内到达角落的路径有几种:EC、EEC、EEEC、EMEC。然后,计算每种路径的概率
这些情况发生时,我们 \( 1 \cdot \frac{1}{2} + 1 \cdot \frac{1}{4} \cdot \frac{1}{2} + 1 \cdot \frac{1}{4} \cdot \frac{1}{2} \cdot \frac{1}{2} + 1 \cdot \frac{1}{4} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{25}{32} \) 有一些答案 ~lceWolf10
解法3(与解法2类似,但分别求出分子和分母)
分别地)
分母
无限制条件下完成4跳共有 \( {4}^{4} = {256} \) 种方式。
分子(分类讨论)
假设弗里达连续跳4次且中途不停。我们按“哪一跳首次到达角落”进行分类讨论。
(1) 第 \( \# 2 \) 跳(第 \( \# 3 \) 跳和第 \( \# 4 \) 跳无限制)
4次独立跳跃分别有4、2、4、4种选择,因此该情形共有 \( 4 \cdot 2 \cdot 4 \cdot 4 = {128} \) 种方式。
(2) 第 \( \# 3 \) 跳(第 \( \# 4 \) 跳无限制)
无论第一跳朝哪个方向,第二跳都必须“绕回”。
4次独立跳跃分别有4、1、2、4种选择,因此该情形共有 \( 4 \cdot 1 \cdot 2 \cdot 4 = {32} \) 种方式。
(3) 第4跳(两个子情形)
(3.1) 第二跳“绕回”,于是第三跳也必须“绕回”。
4次独立跳跃分别有4、1、1、2种选择,因此该子情形共有 \( 4 \cdot 1 \cdot 1 \cdot 2 = 8 \) 种方式。
(3.2) 第二跳回到中心。
4次独立跳跃分别有4、1、4、2种选择,因此该子情形共有 \( 4 \cdot 1 \cdot 4 \cdot 2 = {32} \) 种方式。
综上,情形(3)共有 \( 8 + {32} = {40} \) 种方式。
总计
分子为 \( {128} + {32} + {40} = {200} \) 。
概率
所求概率为 \( \frac{200}{256} = \) (D) \( \frac{25}{32} \) 。
这个问题与1995年AIME第3题非常相似:
https://artofproblemsolving.com/wiki/index.php/1995_AIME_Problems/Problem_3
~热情
解决方案 4
设 \( {C}_{n} \) 为Frieda在第n步后位于中心格的概率, \( {E}_{n} \) 为Frieda在第n步后位于四条边中格的概率, \( {V}_{n} \) (V表示顶点)为Frieda在第n步后位于角格的概率。到达中心格的唯一方式是从边中格沿4个可能方向中的1个特定方向移动,因此 \( {C}_{n + 1} = \frac{{E}_{n}}{4} \) 。到达边中格的方式可以是从中心格沿任意方向移动,或从边中格沿1个特定方向移动,因此 \( {E}_{n + 1} = {C}_{n} + \frac{{E}_{n}}{4} \) 。到达角格的方式可以是到达后停留在原地,或从边中格沿2个特定方向移动,因此 \( {V}_{n + 1} = {V}_{n} + \frac{{E}_{n}}{2} \) 。由于Frieda始终从中心格出发, \( {C}_{0} = 1 \) 、 \( {E}_{0} = 0 \) 和 \( {V}_{0} = 0 \) 。我们利用上述公式计算 \( {V}_{4} \) ,得到 \( \left( D\right) \frac{25}{32} \) 。 -SmileKat32
解决方案 5
想象一个由2×2正方形构成的无限网格,其中每个2×2正方形的中心都位于所有整数有序对(x, y)对应的(3x,3y)处。
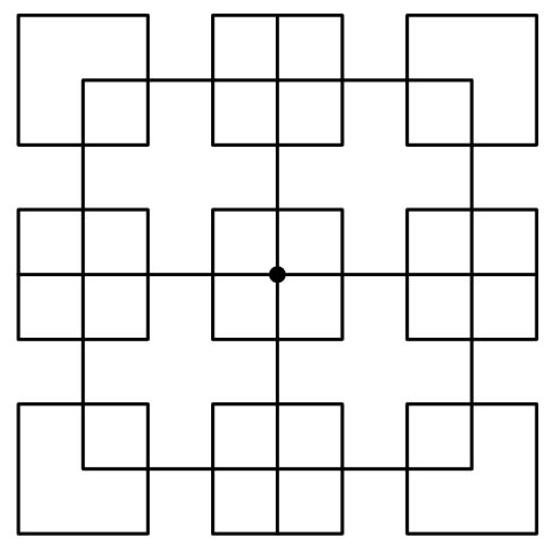
容易看出,这个问题等价于Frieda从(0,0)出发,在这个无限网格上向左、右、上或下移动(除去瞬移)。由于计算补集更容易,我们将计算Frieda在4步内从未到达任何角点的路径数量。
换言之,由于可达的角点仅为 \( \left( {\pm 1, \pm 1}\right) ,\left( {\pm 1, \pm 2}\right) ,\left( {\pm 2, \pm 1}\right) , \) 和 \( \left( {\pm 2, \pm 2}\right) , \) ,Frieda只能沿着包含在 \( S \) 中的点集移动,其中 \( S \) 是 \( x = 0 \) 和 \( y = 0 \) 上满足 \( \left| y\right| < 4 \) 和 \( \left| x\right| < 4 \) 的所有点,再加上以 \( \left( {0,0}\right) . \) 为中心、边长为6的大正方形上的所有点。接下来我们可以进行分情况讨论:
案例1:弗里达既未到达 \( \left( {0, \pm 3}\right) \) ,也未到达 \( \left( {\pm 3,0}\right) . \)
当弗里达在四次移动中仅沿水平或垂直方向移动时,每种情况有 \( {2}^{4} - 4 = {12} \) 种方式。因此,保持同一方向的子情况共有 \( {12} \cdot 2 \) 条路径。(例如,所有长度为4的 \( F \) 和 \( B \) 组合,除去 \( {FFFF},{BBBB},{FFFB} \) ,以及水平方向的 \( {BBBF} \) 。)
还有另一种子情况,她在路径中改变方向。根据弗里达(Frieda)贴近的四个象限中的哪一个,该子情况共有四种对称情形。对于第一象限,可能的路径为 \( F{BUD} \) 、 \( F{BUU} \) 、 \( U{DFB} \) 和 \( U{DFF} \) 。因此,该子情况共有 \( 4 \cdot 4 = {16} \) 种方式。
案例1总计: \( {24} + {16} = {40} \)
情况2:Frieda到达 \( \left( {0, \pm 3}\right) \) 或 \( \left( {\pm 3,0}\right) \) 。
一旦Frieda通过三步到达上述任一位置,她最后一步有四种选择。因此,这种情况共有 \( 4 \cdot 4 = {16} \) 条路径。
因此,我们从不经过角落的总路径数为 \( {16} + {40} = {56}, \) ,从而得到答案
\[ \frac{{4}^{4} - {56}}{{4}^{4}} = {\left( D\right) }^{2}\frac{25}{32}. \]
-fidgetboss_4000
解法6(分情况讨论)
我们根据到达角落所需的跳跃次数分情况讨论。为简化,记 \( E \) 为将Frieda带到边缘的移动, \( W \) 为环绕移动, \( C \) 为角落移动。同时,记 \( O \) 为将我们带回中心的移动。
2跳
此时,Frieda的移动组合必须为(E, C)。有4种方式移动到边缘,2个角落可选,因此共有 \( 4 \cdot 2 = 8 \) 种情况。然后,每一步有4种选择,概率为 \( \frac{8}{4 \cdot 4} = \frac{1}{2} \) 。3跳
2021/3/7 Art of Problem Solving
在这种情况下,Frieda必须环绕。只有一种可能的组合,即(E, W, C)。有4种方式移动到边缘,1种环绕方式(必须沿同一方向继续),2个角落可选,因此共有 \( 4 \cdot 1 \cdot 2 = 8 \) 种情况。然后,每一步有4种选择,概率为 \( \frac{8}{4 \cdot 4 \cdot 4} = \frac{1}{8} \) 。
4跳
最后,这里有两种情况需要考虑。第一种是(E, O, E, C),第二种是第一种情况,有4种方式移动到边缘,1种方式返回中心,4种方式再次移动到边缘,2种方式移动到角落。因此,共有情况。然后,第二种情况,有4种方式移动到角落,1种环绕方式,再次1种环绕方式,2种方式移动到角落。这意味着共有情况。因此,共有情况,总情况为,概率为。于是,Frieda最终落在角落的总概率为~rocketsri
解法7
我将3×3网格表示为
- HOME方格(x1)
- CORN方格(x4)
- 侧边(SIDE)方格(共4个)的转移:
- 主区(HOME)总是移动到侧边(SIDE)
- 角区(CORN)已完成
- 侧边(SIDE)移动到角区(CORN)并伴随移动到侧边(SIDE),再伴随移动到角区(CORN)。移动一次后,将位于方格;移动两次后,将位于;移动三次后,将位于;移动四次后,位于角区(CORN)的概率为
2021 AMC 10A 试题/第24题
题目
某四边形的内部由 \( {\left( x + ay\right) }^{2} = 4{a}^{2} \) 和 \( {\left( ax - y\right) }^{2} = {a}^{2} \) 的图像围成,其中 \( a \) 为正实数。求该区域面积用 \( a \) 表示的表达式,且对所有 \( a > 0 \) 均成立。
(A) \( \frac{8{a}^{2}}{{\left( a + 1\right) }^{2}} \) (B) \( \frac{4a}{a + 1} \) (C) \( \frac{8a}{a + 1} \) (D) \( \frac{8{a}^{2}}{{a}^{2} + 1} \) (E) \( \frac{8a}{{a}^{2} + 1} \)
图示
Desmos 图像:https://www.desmos.com/calculator/satawguqsc
~MRENTHUSIASM
解法1
条件 \( {\left( x + ay\right) }^{2} = 4{a}^{2} \) 和 \( {\left( ax - y\right) }^{2} = {a}^{2} \) 给出 \( \left| {x + {ay}}\right| = \left| {2a}\right| \) 和 \( \left| {{ax} - y}\right| = \left| a\right| \) 或 \( x + {ay} = \pm {2a} \) 和 \( {ax} - y = \pm a \) 。此处斜率互相垂直,因此该四边形为矩形。代入 \( a = 1 \) 并绘制图像,我们很快发现面积为 \( 2\sqrt{2} \cdot \sqrt{2} = 4 \) ,于是通过测试其给出的数值可排除 \( A \) 和 \( B \) (亲自验证!)。再代入 \( a = 2 \) ,我们用直尺测得矩形两边分别约为 \( \frac{7}{4} \) 和 \( \frac{7}{2} \) ,因此面积约为 \( \frac{49}{8} = {6.125} \) 。测试 \( C \) 得 \( \frac{16}{3} \) ,显然小于6,故排除。测试 \( D \) 得 \( \frac{32}{5} \) ,接近我们的答案,故保留。测试 \( E \) 得 \( \frac{16}{5} \) ,远小于6,故排除。因此唯一合理的答案是 \( D \) -firebolt360
解法2(分类讨论)
对于方程 \( {\left( x + ay\right) }^{2} = 4{a}^{2} \) ,情况如下
(1) \( x + {ay} = {2a} \) 。这是一条直线,其 \( x \) 截距为 \( {2a}, y \) ,截距为2,斜率为 \( - \frac{1}{a} \) 。
(2) \( x + {ay} = - {2a} \) 。这是一条具有 \( x \) 截距 \( - {2a}, y \) -截距-2,斜率为 \( - \frac{1}{a} \) 的直线。
对于方程 \( {\left( ax - y\right) }^{2} = {a}^{2} \) ,情况如下
\( \left( {1}^{\prime }\right) {ax} - y = a \) 。这是一条直线,其 \( x \) 截距为 \( 1, y \) , \( - a, \) 截距为 \( a \) ,斜率为
\( \left( {2}^{\prime }\right) {ax} - y = - a \) 。这是一条直线,其 \( x \) 截距为 \( - 1, y \) , \( a, \) 截距为 \( a \) ,斜率为
将 \( a = 2 \) 代入选项得到
(A) \( \frac{32}{9} \) (B) \( \frac{8}{3} \) (C) \( \frac{16}{3} \) (D) \( \frac{32}{5} \) (E) \( \frac{16}{5} \)
将 \( a = 2 \) 代入上述四个方程,并求解相交直线 \( \lbrack \left( 1\right) \) 、 \( \left( {1}^{\prime }\right) ,\left( 1\right) \) 、 \( \left( {2}^{\prime }\right) ,\left( 2\right) \) 、 \( \left( {1}^{\prime }\right) ,\left( 2\right) \) 和 \( \left( {2}^{\prime }\right) \) 的方程组,我们得到各自的解
\[ \left( {x, y}\right) = \left( {\frac{8}{5},\frac{6}{5}}\right) ,\left( {0,2}\right) ,\left( {-\frac{8}{5}, - \frac{6}{5}}\right) ,\left( {0, - 2}\right) . \]
解法2.1(矩形)
由于相交直线(来自上述四个方程)的斜率互为负倒数,该四边形为矩形。最后,根据距离公式,矩形的长和宽分别为 \( \frac{8\sqrt{5}}{5} \) 和 \( \frac{4\sqrt{5}}{5} \) 。我们要求的面积为
\[ \left( \frac{8\sqrt{5}}{5}\right) \left( \frac{4\sqrt{5}}{5}\right) = \frac{32}{5}. \]
答案是 \( \sigma 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda 5\lambda {A}^{2}\lambda {A}^{2}\lambda {A}^{2}\lambda : \lambda : \lambda \)
~MRENTHUSIASM
解法2.2(鞋带公式)
即使我们没有意识到这些解构成矩形的顶点,我们也可以对连续顶点应用鞋带公式
\[ \left( {{x}_{1},{y}_{1}}\right) = \left( {\frac{8}{5},\frac{6}{5}}\right) , \]
\[ \left( {{x}_{2},{y}_{2}}\right) = \left( {0,2}\right) \text{,} \]
\[ \left( {{x}_{3},{y}_{3}}\right) = \left( {-\frac{8}{5}, - \frac{6}{5}}\right) , \]
\[ \left( {{x}_{4},{y}_{4}}\right) = \left( {0, - 2}\right) \text{.} \]
面积公式为
\[ A = \frac{1}{2}\left| {\left( {{x}_{1}{y}_{2} + {x}_{2}{y}_{3} + {x}_{3}{y}_{4} + {x}_{4}{y}_{1}}\right) - \left( {{y}_{1}{x}_{2} + {y}_{2}{x}_{3} + {y}_{3}{x}_{4} + {y}_{4}{x}_{1}}\right) }\right| \]
\[ = \frac{1}{2}\left| {\left\lbrack {\frac{8}{5} \cdot 2 + 0 \cdot \left( {-\frac{6}{5}}\right) + \left( {-\frac{8}{5}}\right) \cdot \left( {-2}\right) + 0 \cdot \frac{6}{5}}\right\rbrack - \left\lbrack {\frac{6}{5} \cdot 0 + 2 \cdot \left( {-\frac{8}{5}}\right) + \left( {-\frac{6}{5}}\right) \cdot 0 + \left( {-2}\right) \cdot \frac{8}{5}}\right\rbrack }\right| \]
\[ = \frac{1}{2}\left| {\left\lbrack {\frac{16}{5} + \frac{16}{5}}\right\rbrack - \left\lbrack {-\frac{16}{5} - \frac{16}{5}}\right\rbrack }\right| \]
\[ = \frac{1}{2}\left| \frac{64}{5}\right| \]
\[ = \frac{32}{5}\text{. } \]
因此,答案是 \( \sigma \) (D) \( \frac{8{a}^{2}}{{a}^{2} + 1} \) 。
鞋带公式推荐阅读:https://artofproblemsolving.com/wiki/index.php/Shoelace_Theorem 2021/3/7 Art of Problem Solving
\[ = {8a} \cdot \frac{1}{\sqrt{{a}^{2} + 1}} \cdot \frac{a}{\sqrt{{a}^{2} + 1}} \]
\[ = \left( {\text{ }\mathbf{D}\text{ }}\right) \frac{8{a}^{2}}{{a}^{2} + 1}. \]
(注: \( \tan A = \) 斜率 \( a \) )
-fnothing4994
解法4(“bruh moment”解法)
尝试 \( a = 1 \) 可将选项缩小至(C)、(D)和(E)。再尝试 \( a = 2 \) 和 \( a = 3 \) 可排除(C)和(E),
从而得到 \( \left| {\left( \mathrm{D}\right) \frac{8{a}^{2}}{{a}^{2} + 1}}\right| \) 作为答案。-¢
2021 AMC 10A 第25题
题目
在一个 \( 3 \times 3 \) 的方格网中,有多少种方法放置3个不可区分的红色筹码、3个不可区分的蓝色筹码和3个不可区分的绿色筹码,使得任意两个同色筹码在垂直或水平方向上都不直接相邻?
(A) 12 (B) 18 (C) 24 (D) 30 (E) 36
解法1
将不同颜色记为A、B、C。共有 \( 3! = 6 \) 种方式将这些颜色重新分配给这三个字母,因此在网格中排列字母后需乘以6。不妨设A位于中心。
? ? ?
? A ?
? ? ?
在此配置下,有两种情况:要么所有A都位于同一条对角线上:
 | ||
 | ||
 |
或者另外两个A位于相邻的角上:
 |  |  |
 |  |  |
 |  |  |
在第一种情况下,由于有两条对角线,因此有两种排列方式;在第二种情况下,由于有四对相邻的角,因此有四种排列方式。在每种情况下,三个B和三个C都只有如图示所示的一种放置方式。这意味着在网格中排列A、B和C共有 \( 4 + 2 = 6 \) 种方式,而颜色有6种重新排列方式。因此,总共有 \( 6 \cdot 6 = {36} \) 种方式,即 \( \left| E\right| \)

-happykeeper
解法2(分类讨论)
不失一般性,我们在左上角放置一个红球。有两种情况:
情况(1):与左上角红球相邻的两个球颜色不同。
| \( \mathbf{R} \) | B | |
| G | \( \mathbf{R} \) |
每种放置方式有6种排列,因为RBG有 \( 3! = 6 \) 种排列方式。
情况(1)有三个子情况:
| R | B | R |
| G | R | G |
| B | G | B |
| R | B | G |
| G | R | B |
| R | B | G |
| R | B | G |
| G | R | B |
| B | G | R |
因此,情况(1)有 \( 3 \cdot 6 = {18} \) 种方式。
情况(2):与左上角红球相邻的两个球颜色相同。
| \( \mathbf{R} \) | B | |
| B |
每种放置方式有6种排列,因为共有 \( \left( \begin{array}{l} 3 \\ 2 \end{array}\right) \left( \begin{array}{l} 2 \\ 1 \end{array}\right) = 6 \) 种方法选出恰好包含两种颜色的三个球(RBB、RGG、BRR、BGG、GRR、GBB)。情况(2)有三个子情况:
| R | B | R |
| B | G | B |
| G | R | G |
| R | B | G |
| B | G | R |
| R | B | G |
| R | B | G |
| B | G | R |
| G | R | B |
因此,情况(2)有 \( 3 \cdot 6 = {18} \) 种方法。综上,答案是 \( {18} + {18} = \) (E)36 ~MRENTHUSIASM
解法3(分类讨论与错位排列)
情况(1):我们将R、B、G作为所有行的一种排列。这三种颜色共有 \( 3! \) 种排列方式。完成第一行后,进入第二行。注意,第二行必须是第一行的错位排列(derangement)。根据错位排列
公式, \( \frac{3!}{e} \approx 2 \) ,因此第二行有2种可能的排列。(注:你也可以通过容斥原理(PIE)求出错位排列
的数量)。最后,最后一行有2种可能的排列。因此,共有 \( 3! \cdot 2 \cdot 2 = {24} \) 种可能性。
情况(2):所有行都有两个球颜色相同,另一个球颜色不同。显然,第一行有3种可能配置,第二行有2种,第三行有2种。 \( 3 \cdot 2 \cdot 2 = {12} \) 。
因此,我们的答案是 \( {24} + {12} = \) (E) 36